Creating a new `Op`: Python implementation#

You may have looked through the library documentation but don’t see a function that does what you want.

If you can implement something in terms of an existing Op, you should do that. A PyTensor function that builds upon existing expressions will be better optimized, automatic differentiable, and work seamlessly across different backends.

However, if you cannot implement an Op in terms of an existing Op, you have to write a new one.

This page will show how to implement some simple Python-based Op that perform operations on numpy arrays.

PyTensor Graphs refresher#

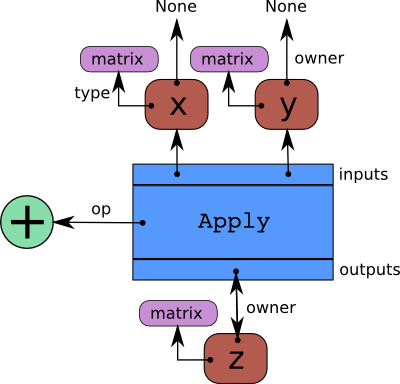
PyTensor represents symbolic mathematical computations as graphs. Those graphs are bi-partite graphs (graphs with two types of nodes), they are composed of interconnected Apply and Variable nodes. Variable nodes represent data in the graph, either inputs, outputs or intermediary values. As such, inputs and outputs of a graph are lists of PyTensor Variable nodes. Apply nodes perform computation on these variables to produce new variables. Each Apply node has a link to an instance of Op which describes the computation to perform. This tutorial details how to write such an Op instance. Please refer to Graph Structures for a more detailed explanation about the graph structure.

`Op`’s basic methods#

An Op is any Python object that inherits from Op. This section provides an overview of the basic methods you typically have to implement to make a new Op. It does not provide extensive coverage of all the possibilities you may encounter or need. For that refer to Op contract.

from typing import Any
from pytensor.graph.basic import Apply, Variable
from pytensor.graph.fg import FunctionGraph
from pytensor.graph.op import Op
from pytensor.graph.type import Type


class MyOp(Op):
    # Properties attribute
    __props__ : tuple[Any, ...] = ()

    # Constructor, usually used only to set Op properties
    def __init__(self, *args):
        pass

    # itypes and otypes attributes are compulsory if make_node method is not defined.
    # They're the type of input and output respectively
    itypes: list[Type] | None = None
    otypes: list[Type] | None = None

    # make_node is compulsory if itypes and otypes are not defined
    # make_node is more flexible: output types can be determined
    # based on the input types and Op properties.
    def make_node(self, *inputs) -> Apply:
        pass

    # Performs the numerical evaluation of Op in Python. Required.
    def perform(self, node: Apply, inputs_storage: list[Any], output_storage: list[list[Any]]) -> None:
        pass

    # Defines the symbolic expression for the L-operator based on the input and output variables
    # and the output gradient variables. Optional.
    def L_op(self, inputs: list[Variable], outputs: list[Variable], output_grads: list[Variable]) -> list[Variable]:
        pass

    # Equivalent to L_op, but with a "technically"-bad name and without outputs provided.
    # It exists for historical reasons. Optional.
    def grad(self, inputs: list[Variable], output_grads: list[Variable]) -> list[Variable]:
        # Same as self.L_op(inputs, self(inputs), output_grads)
        pass

    # Defines the symbolic expression for the R-operator based on the input variables
    # and eval_point variables. Optional.
    def R_op(self, inputs: list[Variable], eval_points: list[Variable | None]) -> list[Variable | None]:
        pass

    # Defines the symbolic expression for the output shape based on the input shapes
    # and, less frequently, the input variables via node.inputs. Optional.
    def infer_shape(self, fgraph: FunctionGraph, node: Apply, input_shapes: list[tuple[Variable, ...]]) -> list[tuple[Variable]]:
        pass

An Op has to implement some methods defined in the the interface of Op. More specifically, it is mandatory for an Op to define either the method make_node() or itypes, otypes, and perform().

`make_node()`#

make_node() method creates an Apply node representing the application of the Op on the inputs provided. This method is responsible for three things:

Checks that the inputs can be converted to Variables whose types are compatible with the current Op. If the Op cannot be applied on the provided input types, it must raise an exception (such as TypeError).
Creates new output Variables of a suitable symbolic Type to serve as the outputs of this Op’s application.
Returns an Apply instance with the input and output Variables, and itself as the Op.

If make_node() is not defined, the itypes and otypes are used by the Op’s make_node() method to implement the functionality method mentioned above.

`perform()`#

perform() method defines the Python implementation of an Op. It takes several arguments:

node is a reference to an Apply node which was previously obtained via the make_node() method. It is typically not used in a simple Op, but it contains symbolic information that could be required by a complex Op.
inputs is a list of references to data which can be operated on using non-symbolic statements, (i.e., statements in Python, Numpy).
output_storage is a list of storage cells where the output is to be stored. There is one storage cell for each output of the Op. The data put in output_storage must match the type of the symbolic output. PyTensor may sometimes allow output_storage elements to persist between evaluations, or it may reset output_storage cells to hold a value of None. It can also pre-allocate some memory for the Op to use. This feature can allow perform to reuse memory between calls, for example. If there is something preallocated in the output_storage, it will be of the correct dtype, but can have the wrong shape and have any stride pattern.

perform() method must be determined by the inputs. That is to say, when applied to identical inputs the method must return the same outputs.

`Op`’s auxiliary methods#

There are other methods that can be optionally defined by the Op:

`props`#

The __props__ attribute lists the Op instance properties that influence how the computation is performed. It must be a hashable tuple. Usually these are set in __init__(). If you don’t have any properties that influence the computation, then you will want to set this attribute to the empty tuple ().

__props__ enables the automatic generation of appropriate __eq__() and __hash__(). According to this default, __eq__(), two Ops will be equal if they have the same values for all the properties listed in __props__. Similarly, they will have the same hash.

When PyTensor sees two nodes with equal Ops and the same set of inputs, it will assume the outputs are equivalent and merge the nodes to avoid redundant computation. When Op.__props__ is not specified, two distinct instances of the same class will not be equal and hash to their id. PyTensor won’t merge nodes with the same class but different instances in this case.

__props__ will also generate a suitable __repr__() and __str__() for your Op.

`infer_shape()`#

The infer_shape() method allows an Op to infer the shape of its output variables without actually computing them. It takes as input fgraph, a FunctionGraph; node, a reference to the Op’s Apply node; and a list of Variabless (e.g. i0_shape, i1_shape, …) which are the dimensions of the Op input Variables. infer_shape() returns a list where each element is a tuple representing the shape of one output. This could be helpful if one only needs the shape of the output instead of the actual outputs, which can be useful, for instance, for rewriting procedures.

`L_op()`#

The L_op() method is required if you want to differentiate some cost whose expression includes your Op. The gradient is specified symbolically in this method. It takes three arguments inputs, outputs and output_gradients, which are both lists of Variables, and those must be operated on using PyTensor’s symbolic language. The L_op() method must return a list containing one Variable for each input. Each returned Variable represents the gradient with respect to that input computed based on the symbolic gradients with respect to each output.

If the output is not differentiable with respect to an input then this method should be defined to return a variable of type NullType for that input. Likewise, if you have not implemented the gradient computation for some input, you may return a variable of type NullType for that input. Please refer to L_op() for a more detailed view.

`R_op()`#

The R_op() method is needed if you want pytensor.gradient.Rop() to work with your Op.

This function implements the application of the R-operator on the function represented by your Op. Let’s assume that function is \(f\), with input \(x\), applying the R-operator means computing the Jacobian of \(f\) and right-multiplying it by \(v\), the evaluation point, namely: \(\frac{\partial f}{\partial x} v\).

Example: `Op` definition#

import numpy as np
from pytensor.graph.op import Op
from pytensor.graph.basic import Apply, Variable
from pytensor.tensor import as_tensor_variable, TensorLike, TensorVariable

class DoubleOp1(Op):
    __props__ = ()

    def make_node(self, x: TensorLike) -> Apply:
        # Convert (and require) x to be a TensorVariable
        x = as_tensor_variable(x)

        # Validate input type
        if not(x.type.ndim == 2 and x.type.dtype == "float64"):
            raise TypeError("x must be a float64 matrix")

        # Create an output variable of the same type as x
        z = x.type()

        # TensorVariables type include shape and dtype, so this is equivalent to the following
        # z = pytensor.tensor.TensorType(dtype=x.type.dtype, shape=x.type.shape)()
        # z = pytensor.tensor.tensor(dtype=x.type.dtype, shape=x.type.shape)
        return Apply(self, [x], [z])

    def perform(self, node: Apply, inputs: list[np.ndarray], output_storage: list[list[np.ndarray | None]]) -> None:
        x = inputs[0]
        z = output_storage[0]
        # Numerical output based on numerical inputs (i.e., numpy arrays)
        z[0] = x * 2

    def infer_shape(self, fgraph: FunctionGraph, node: Apply, input_shapes: list[list[Variable]]) -> list[list[Variable]]:
        # The output shape is the same as the input shape
        return input_shapes

    def L_op(self, inputs: list[TensorVariable], outputs: list[TensorVariable], output_grads: list[TensorVariable]):
        # Symbolic expression for the gradient
        # For this Op, the inputs and outputs aren't part of the expression
        # output_grads[0] is a TensorVariable!
        return [output_grads[0] * 2]

    def R_op(self, inputs: list[TensorVariable], eval_points: list[TensorVariable | None]) -> list[TensorVariable] | None:
        # R_op can receive None as eval_points.
        # That means there is no differentiable path through that input
        # If this imply that you cannot compute some outputs,
        # return None for those.
        if eval_points[0] is None:
            return None
        # For this Op, the R_op is the same as the L_op
        outputs = self(inputs)
        return self.L_op(inputs, outputs, eval_points)

doubleOp1 = DoubleOp1()

At a high level, the code fragment declares a class (e.g., DoubleOp1) and then creates one instance of that class (e.g., doubleOp1).

As you’ll see below, you can then pass an instantiated Variable, such as x = tensor.matrix("x") to the instantiated Op, to define a new Variable that represents the output of applying the Op to the input variable.

Under the hood, the __call__() will call make_node() method and then returns the output variable(s) of the Apply that is returned by the method.

The number and order of the inputs argument in the returned Apply should match those in the make_node(). PyTensor may decide to call make_node() itself later to copy the graph or perform a generic rewrite.

All the inputs and outputs arguments to the returned Apply must be Variables. A common and easy way to ensure inputs are variables is to run them through as_tensor_variable. This function leaves TensorVariable variables alone, raises an error for variables with an incompatible type, and copies any numpy.ndarray into the storage for a TensorConstant.

The perform() method implements the Op’s mathematical logic in Python. The inputs (here x = inputs[0]) are passed by value, and a single output is stored as the first element of a single-element list (here z = output_storage[0]). If doubleOp1 had a second output, it should be stored in output_storage[1][0].

In some execution modes, the output storage might contain the return value of a previous call. That old value can be reused to avoid memory re-allocation, but it must not influence the semantics of the Op output.

You can try the new Op as follows:

from pytensor import function
from pytensor.tensor import matrix

doubleOp1 = DoubleOp1()

x = matrix("x")
out = doubleOp1(x)
assert out.type == x.type

fn = function([x], out)
x_np = np.random.normal(size=(5, 4))
np.testing.assert_allclose(x_np * 2, fn(x_np))

It’s also a good idea to test the infer_shape() implementation. To do this we can request a graph of the shape only:

out_shape = out.shape
shape_fn = function([x], out_shape)
assert tuple(shape_fn(x_np)) == x_np.shape

# We can introspect the compiled function to confirm the Op is not evaluated
shape_fn.dprint()

MakeVector{dtype='int64'} [id A] 2
 ├─ Shape_i{0} [id B] 1
 │  └─ x [id C]
 └─ Shape_i{1} [id D] 0
    └─ x [id C]

Finally we should test the gradient implementation. For this we can use the pytensor.gradient.verify_grad utility which will compare the output of a gradient function with finite differences.

rng = np.random.default_rng(42)
test_x = rng.normal(size=(5, 4))

# Raises if the gradient output is sufficiently different from the finite difference approximation.
verify_grad(doubleOp1, [test_x], rng=rng)

Example: `itypes` and `otypes` definition#

Since the Op has a very strict type signature, we can use itypes and otypes instead of make_node():

from pytensor.tensor import dmatrix

class DoubleOp2(Op):
    __props__ = ()

    # inputs and output types must be float64 matrices
    itypes = [dmatrix]
    otypes = [dmatrix]

    def perform(self, node, inputs, output_storage):
        x = inputs[0]
        z = output_storage[0]
        z[0] = x * 2

doubleOp2 = DoubleOp2()

Example: `props` definition#

We can modify the previous piece of code in order to demonstrate the usage of the __props__ attribute.

We create an Op that takes a variable x and returns a*x+b. We want to say that two such Ops are equal when their values of a and b are equal.

from pytensor.graph.op import Op
from pytensor.graph.basic import Apply
from pytensor.tensor import as_tensor_variable

class AXPBOp(Op):
    """
    This creates an Op that takes x to a*x+b.
    """
    __props__ = ("a", "b")

    def __init__(self, a, b):
        self.a = a
        self.b = b
        super().__init__()

    def make_node(self, x):
        x = as_tensor_variable(x)
        return Apply(self, [x], [x.type()])

    def perform(self, node, inputs, output_storage):
        x = inputs[0]
        z = output_storage[0]
        z[0] = self.a * x + self.b

The use of __props__ saves the user the trouble of implementing __eq__() and __hash__() manually. It also generates default __repr__() and __str__() methods that prints the attribute names and their values.

We can test this by running the following segment:

import numpy as np
from pytensor.tensor import matrix
from pytensor import function

mult4plus5op = AXPBOp(4, 5)
another_mult4plus5op = AXPBOp(4, 5)
mult2plus3op = AXPBOp(2, 3)

assert mult4plus5op == another_mult4plus5op
assert mult4plus5op != mult2plus3op

x = matrix("x", dtype="float32")
f = function([x], mult4plus5op(x))
g = function([x], mult2plus3op(x))

inp = np.random.normal(size=(5, 4)).astype("float32")
np.testing.assert_allclose(4 * inp + 5, f(inp))
np.testing.assert_allclose(2 * inp + 3, g(inp))

To demonstrate the use of equality, we will define the following graph: mult4plus5op(x) + another_mult4plus5op(x) + mult3plus2op(x). And confirm PyTensor infers it can reuse the first term in place of the second another_mult4plus5op(x).

from pytensor.graph import rewrite_graph

graph = mult4plus5op(x) + another_mult4plus5op(x) + mult2plus3op(x)
print("Before:")
graph.dprint()

print("\nAfter:")
rewritten_graph = rewrite_graph(graph)
rewritten_graph.dprint()

After:
Add [id A]
 ├─ AXPBOp{a=4, b=5} [id B]
 │  └─ x [id C]
 ├─ AXPBOp{a=4, b=5} [id B]
 │  └─ ···
 └─ AXPBOp{a=2, b=3} [id D]
    └─ x [id C]

Note how after rewriting, the same variable [id B] is used twice. Also the string representation of the Op shows the values of the properties.

Example: More complex `Op`#

As a final example, we will create a multi-output Op that takes a matrix and a vector and returns the matrix transposed and the sum of the vector.

Furthermore, this Op will work with batched dimensions, meaning we can pass in a 3D tensor or a 2D tensor (or more) and it will work as expected. To achieve this behavior we cannot use itypes and otypes as those encode specific number of dimensions. Instead we will have to define the make_node method.

We need to be careful in the L_op() method, as one of output gradients may be disconnected from the cost, in which case we should ignore its contribution. If both outputs are disconnected PyTensor will not bother calling the L_op() method, so we don’t need to worry about that case.

import pytensor.tensor as pt

from pytensor.graph.op import Op
from pytensor.graph.basic import Apply
from pytensor.gradient import DisconnectedType

class TransposeAndSumOp(Op):
    __props__ = ()

    def make_node(self, x, y):
        # Convert to TensorVariables (and fail if not possible)
        x = pt.as_tensor_variable(x)
        y = pt.as_tensor_variable(y)

        # Validate inputs dimensions
        if x.type.ndim < 2:
            raise TypeError("x must be at least a matrix")
        if y.type.ndim < 1:
            raise TypeError("y must be at least a vector")

        # Create output variables
        out1_static_shape = (*x.type.shape[:-2], x.type.shape[-1], x.type.shape[-2])
        out1_dtype = x.type.dtype
        out1 = pt.tensor(dtype=out1_dtype, shape=out1_static_shape)

        out2_static_shape = y.type.shape[:-1]
        out2_dtype = "float64"  # hard-coded regardless of the input
        out2 = pt.tensor(dtype=out2_dtype, shape=out2_static_shape)

        return Apply(self, [x, y], [out1, out2])

    def perform(self, node, inputs, output_storage):
        x, y = inputs
        out_1, out_2 = output_storage
        out_1[0] = np.swapaxes(x, -1, -2)
        out_2[0] = y.sum(-1).astype("float64")

    def infer_shape(self, fgraph, node, input_shapes):
        x_shapes, y_shapes = input_shapes
        out1_shape = (*x_shapes[:-2], x_shapes[-1], x_shapes[-2])
        out2_shape = y_shapes[:-1]
        return [out1_shape, out2_shape]

    def L_op(self, inputs, outputs, output_grads):
        x, y = inputs
        out1_grad, out2_grad = output_grads

        if isinstance(out1_grad.type, DisconnectedType):
            x_grad = DisconnectedType()()
        else:
            # Transpose the last two dimensions of the output gradient
            x_grad = pt.swapaxes(out1_grad, -1, -2)

        if isinstance(out2_grad.type, DisconnectedType):
            y_grad = DisconnectedType()()
        else:
            # Broadcast the output gradient to the same shape as y
            y_grad = pt.broadcast_to(pt.expand_dims(out2_grad, -1), y.shape)

        return [x_grad, y_grad]

Let’s test the Op evaluation:

import numpy as np
from pytensor import function

transpose_and_sum_op = TransposeAndSumOp()

x = pt.tensor("x", shape=(5, None, 3), dtype="float32")
y = pt.matrix("y", shape=(2, 1), dtype="float32")
x_np = np.random.normal(size=(5, 4, 3)).astype(np.float32)
y_np = np.random.normal(size=(2, 1)).astype(np.float32)

out1, out2 = transpose_and_sum_op(x, y)

# Test the output types
assert out1.type.shape == (5, 3, None)
assert out1.type.dtype == "float32"
assert out2.type.shape == (2,)
assert out2.type.dtype == "float64"

# Test the perform method
f = function([x, y], [out1, out2])
out1_np, out2_np = f(x_np, y_np)
np.testing.assert_allclose(out1_np, x_np.swapaxes(-1, -2))
np.testing.assert_allclose(out2_np, y_np.sum(-1))

And the shape inference:

out1_shape = out1.shape
out2_shape = out2.shape
shape_fn = function([x, y], [out1_shape, out2_shape])

out1_shape_np, out2_shape_np = shape_fn(x_np, y_np)
assert tuple(out1_shape_np) == out1_np.shape
assert tuple(out2_shape_np) == out2_np.shape

# We can introspect the compiled function to confirm the Op is not needed
shape_fn.dprint()

MakeVector{dtype='int64'} [id A] 1
 ├─ 5 [id B]
 ├─ 3 [id C]
 └─ Shape_i{1} [id D] 0
    └─ x [id E]
DeepCopyOp [id F] 2
 └─ [2] [id G]

Finally, the gradient expression:

Again, we can use pytensor verify_grad function to test the gradient implementation. Due to the presence of multiple outputs we need to pass a Callable instead of the Op instance. There are different cases we want to test: when both or just one of the outputs is connected to the cost

transpose_and_sum_op = TransposeAndSumOp()

def both_outs_connected(x, y):
    out1, out2 = transpose_and_sum_op(x, y)
    return out1.sum() + out2.sum()

def only_out1_connected(x, y):
    out1, _ = transpose_and_sum_op(x, y)
    return out1.sum()

def only_out2_connected(x, y):
    _, out2 = transpose_and_sum_op(x, y)
    return out2.sum()

rng = np.random.default_rng(seed=37)
x_np = rng.random((5, 4, 3)).astype(np.float32)
y_np = rng.random((2, 1)).astype(np.float32)
verify_grad(both_outs_connected, [x_np, y_np], rng=rng)

# PyTensor will raise a warning about the disconnected gradient
with warnings.catch_warnings():
    warnings.simplefilter("ignore")
    verify_grad(only_out1_connected, [x_np, y_np], rng=rng)
    verify_grad(only_out2_connected, [x_np, y_np], rng=rng)

We are filtering a warning about DisconnectTypes being returned by the gradient method. PyTensor would like to know how the outputs of the Op are connected to the input, which could be done with connection_pattern This was omitted for brevity, since it’s a rare edge-case.

Developer testing utilities#

PyTensor has some functionalities to test for a correct implementation of an Op and it’s many methods.

We have already seen some user-facing helpers, but there are also test classes for Op implementations that are added to the codebase, to be used with pytest.

Here we mention those that can be used to test the implementation of:: infer_shape() L_op() R_op()

Basic Tests#

Basic tests are done by you just by using the Op and checking that it returns the right answer. If you detect an error, you must raise an exception.

You can use the assert keyword to automatically raise an AssertionError, or utilities in numpy.testing.

import numpy as np
from pytensor import function
from pytensor.tensor import matrix
from tests.unittest_tools import InferShapeTester


class TestDouble(InferShapeTester):
    def setup_method(self):
        super().setup_method()
        self.op_class = DoubleOp
        self.op = DoubleOp()

    def test_basic(self):
        rng = np.random.default_rng(377)

        x = matrix("x", dtype="float64")
        f = pytensor.function([x], self.op(x))

        inp = np.asarray(rng.random((5, 4)), dtype="float64")
        out = f(inp)

        # Compare the result computed to the expected value.
        np.testing.assert_allclose(inp * 2, out)

Testing the `infer_shape()`#

When a class inherits from the InferShapeTester class, it gets the InferShapeTester._compile_and_check() method that tests the infer_shape() method. It tests that the Op gets rewritten out of the graph if only the shape of the output is needed and not the output itself. Additionally, it checks that the rewritten graph computes the correct shape, by comparing it to the actual shape of the computed output.

InferShapeTester._compile_and_check() compiles an PyTensor function. It takes as parameters the lists of input and output PyTensor variables, as would be provided to pytensor.function(), and a list of real values to pass to the compiled function. It also takes the Op class as a parameter in order to verify that no instance of it appears in the shape-optimized graph.

If there is an error, the function raises an exception. If you want to see it fail, you can implement an incorrect infer_shape().

When testing with input values with shapes that take the same value over different dimensions (for instance, a square matrix, or a tensor3 with shape (n, n, n), or (m, n, m)), it is not possible to detect if the output shape was computed correctly, or if some shapes with the same value have been mixed up. For instance, if the infer_shape() uses the width of a matrix instead of its height, then testing with only square matrices will not detect the problem. To avoid this the InferShapeTester._compile_and_check() method prints a warning in such a case. If your Op works only with such matrices, you can disable the warning with the warn=False parameter.

class TestDouble(InferShapeTester):

    # [...] as previous tests.

    def test_infer_shape(self):
        rng = np.random.default_rng(42)
        x = matrix("x", dtype="float64")
        self._compile_and_check(
            [x],  # pytensor.function inputs
            [self.op(x)],  # pytensor.function outputs
            # Non-square inputs
            [rng.random(size=(5, 4))],
            # Op that should be removed from the graph.
            self.op_class,
        )

Testing the gradient#

As shown above, the function verify_grad verifies the gradient of an Op or PyTensor graph. It compares the analytic (symbolically computed) gradient and the numeric gradient (computed through the Finite Difference Method).

If there is an error, the function raises an exception. If you want to see it fail, you can implement an incorrect gradient (for instance, by removing the multiplication by 2).

def test_grad(self):
    rng = np.random.default_rng(2024)
    verify_grad(
        self.op,
        [rng.random(size=(5, 7, 2))],
        rng = rng,
    )

Testing the Rop#

The class RopLopChecker defines the methods RopLopChecker.check_mat_rop_lop(), RopLopChecker.check_rop_lop() and RopLopChecker.check_nondiff_rop(). These allow to test the implementation of the R_op() method of a particular Op.

For instance, to verify the R_op() method of the DoubleOp, you can use this:

import numpy
import tests
from tests.test_rop import RopLopChecker

class TestDoubleOpRop(RopLopChecker):

    def test_double_rop(self):
        self.check_rop_lop(DoubleOp()(self.x), self.in_shape)

Running Your Tests#

To perform your tests, simply run pytest.

Exercise#

Run the code of the DoubleOp example above.

Modify and execute to compute: x * y.

Modify and execute the example to return two outputs: x + y and jx - yj.

You can omit the Rop() functions. Try to implement the testing apparatus described above.

Solution

`wrap_py()`#

wrap_py() is a Python decorator that converts a Python function into a basic PyTensor Op that will call the supplied function during execution.

This isn’t the recommended way to build an Op, but allows for a quick implementation.

It takes an optional infer_shape() parameter that must have this signature:

  def infer_shape(fgraph, node, input_shapes):
      # ...
      return output_shapes

- :obj:`input_shapes` and :obj:`output_shapes` are lists of tuples that
  represent the shape of the corresponding inputs/outputs, and :obj:`fgraph`
  is a :class:`FunctionGraph`.

Warning

Not providing a infer_shape() prevents shape-related rewrites from working with this Op. For example your_op(inputs, ...).shape will need the Op to be executed just to get the shape.

Note

As no L_op is defined, this means you won’t be able to differentiate paths that include this Op.

Note

It converts the Python function to a Callable object that takes as inputs PyTensor variables that were declared.

Note

The python function wrapped by the wrap_py() decorator needs to return a new data allocation, no views or in place modification of the input.

`wrap_py()` Example#

import pytensor
import pytensor.tensor as pt
import numpy as np
from pytensor import function
from pytensor.compile.ops import wrap_py

def infer_shape_numpy_dot(fgraph, node, input_shapes):
    ashp, bshp = input_shapes
    return [ashp[:-1] + bshp[-1:]]


@wrap_py(
    itypes=[pt.dmatrix, pt.dmatrix],
    otypes=[pt.dmatrix],
    infer_shape=infer_shape_numpy_dot,
)
def numpy_dot(a, b):
   return np.dot(a, b)

You can try it as follows:

x = pt.matrix()
y = pt.matrix()
f = function([x, y], numpy_dot(x, y))
inp1 = np.random.random_sample((5, 4))
inp2 = np.random.random_sample((4, 7))
out = f(inp1, inp2)

Final Note#

The section Other Ops includes more instructions for the following specific cases:

Scalar/Elemwise/Reduction Ops

Sparse Ops

OpenMP Ops

For defining C-based COp see Extending PyTensor with a C Op. For defining implementations for other backends see creating_a_numba_jax_op.

Note

This is an introductory tutorial and as such it does not cover how to make an Op that returns a view or modifies the values in its inputs. Thus, all Ops created with the instructions described here MUST return newly allocated memory or reuse the memory provided in the parameter output_storage of the perform() method. See Views and inplace operations for an explanation on how to do this.

If your Op returns a view or changes the value of its inputs without doing as prescribed in that page, PyTensor will run, but will return correct results for some graphs and wrong results for others.

It is recommended that you run your tests in DebugMode, since it can help verify whether or not your Op behaves correctly in this regard.

Creating a new Op: Python implementation#

PyTensor Graphs refresher#

Op’s basic methods#

make_node()#

perform()#

Op’s auxiliary methods#

__props__#

infer_shape()#

L_op()#

R_op()#

Example: Op definition#

Example: itypes and otypes definition#

Example: __props__ definition#

Example: More complex Op#

Developer testing utilities#

Basic Tests#

Testing the infer_shape()#

Testing the gradient#

Testing the Rop#

Running Your Tests#

Exercise#

wrap_py()#

wrap_py() Example#

Final Note#

Creating a new `Op`: Python implementation#

`Op`’s basic methods#

`make_node()`#

`perform()`#

`Op`’s auxiliary methods#

`props`#

`infer_shape()`#

`L_op()`#

`R_op()`#

Example: `Op` definition#

Example: `itypes` and `otypes` definition#

Example: `props` definition#

Example: More complex `Op`#

Testing the `infer_shape()`#

`wrap_py()`#

`wrap_py()` Example#